面试题：堆排序是一种稳定排序吗？

在回答该问题前，首先需要了解什么是稳定排序。

稳定性就是指对于两个关键字相等的记录，它们在序列中的相对位置，在排序之前和排序之后没有发生改变。通俗地讲就是有两个关键字相等的数据A、B，排序前，A的位置是 i ，B的位置是 j，此时 i < j，则如果在排序后A的位置还是在B之前，那么称它是稳定的。

那么堆排序是一个稳定排序吗？

堆排序的稳定性分析

直接上答案堆排序并不是一个稳定排序。

堆排序的会将原始的数组转化成一个大顶堆或一个小顶堆，在输出堆顶后，此时需要维护堆，操作如下：

（1）堆顶与堆尾交换并删除堆尾，被删除的堆尾的元素就是输出过的元素

（2）把当前堆顶向下调整，直到满足构成堆的条件，重复（1）步骤

在堆顶与堆尾交换的时候两个相等的记录在序列中的相对位置就可能发生改变，这就影响其稳定性了。

下面看一个实际的例子， [5,4A,3,2,4B,1] ，A和B用于区分相同元素。

数组的原始的状态如下所示：

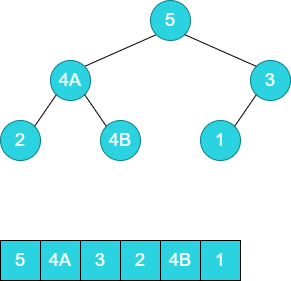
当前状态下，已经是一个大顶堆，因此将堆顶元素5和尾部元素1进行交换.

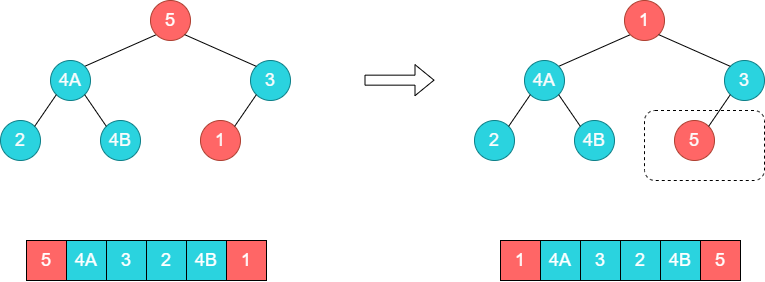
接着调整子树[1，4A，3]，将1和4A的位置调换。

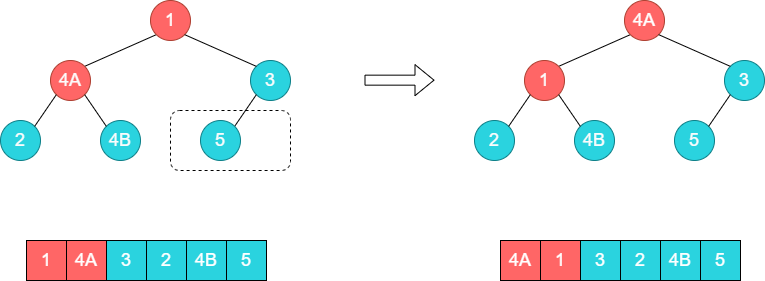
接着调整子树[1，2，4B]，将1和4B的位置调换。

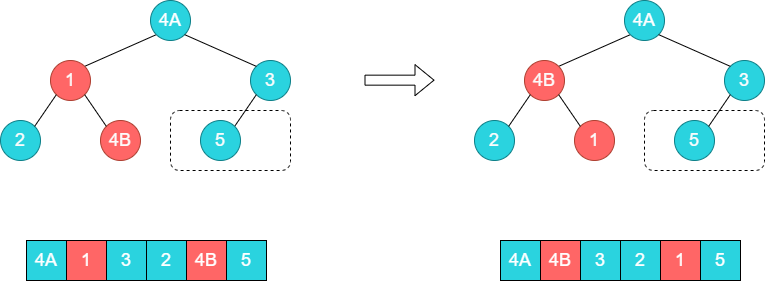
至此，又一轮排序完毕，将4A和数组尾部元素1交换。

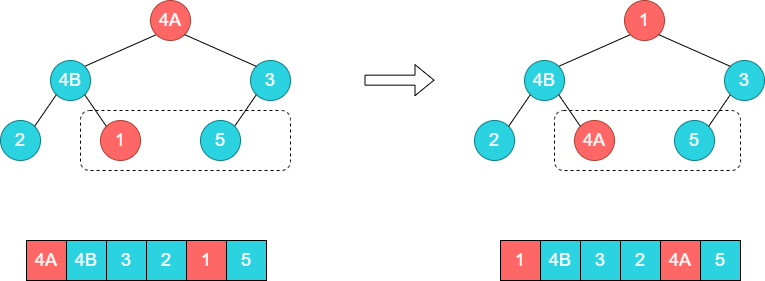
接着调整顶部的子树[1，4B，3]，将1和4B的位置调换。

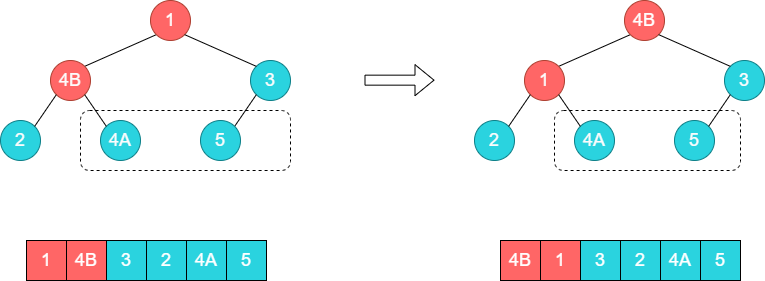
接着调整子树[1，2]，将1和2的位置调换。

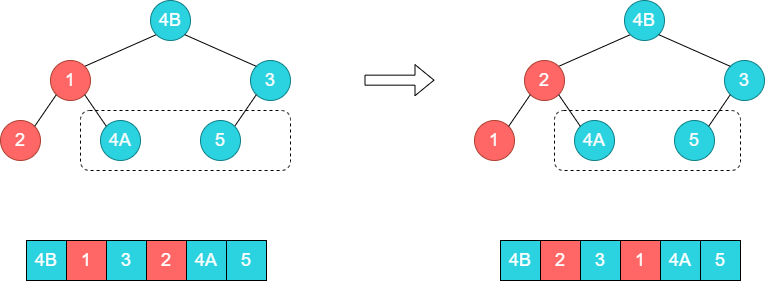
至此，又一轮排序完毕，将4B和数组尾部元素1交换。

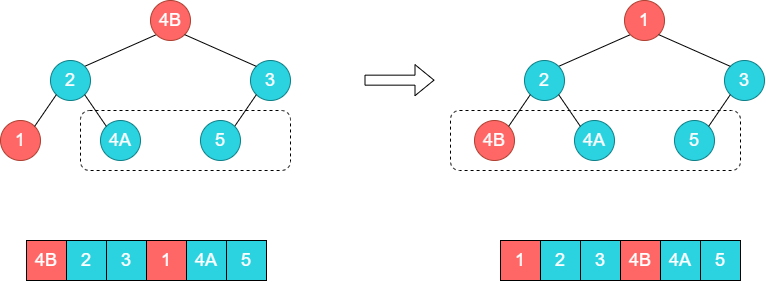
至此为止，元素4B已经排在了4A前面，已经可以证明出堆排序的不稳定性。

通过下面的c++的代码也验证了这一点。

#include <iostream>
#include <vector>
#include <algorithm>

// 打印数组的函数
void printArray(const std::vector<std::pair<int, char>>& arr) {
    for (const auto& elem : arr) {
        std::cout << elem.first << elem.second << " ";
    }
    std::cout << std::endl;
}

// 堆排序的辅助函数，用于堆调整
void heapify(std::vector<std::pair<int, char>>& arr, int n, int i) {
    int largest = i;        // 初始化最大元素为根节点
    int left = 2 * i + 1;   // 左子节点
    int right = 2 * i + 2;  // 右子节点

    // 如果左子节点比根节点大
    if (left < n && arr[left].first > arr[largest].first)
        largest = left;

    // 如果右子节点比当前最大元素大
    if (right < n && arr[right].first > arr[largest].first)
        largest = right;

    // 如果最大元素不是根节点
    if (largest != i) {
        std::swap(arr[i], arr[largest]);

        // 递归地对受影响的子树进行堆调整
        heapify(arr, n, largest);
    }
}

// 堆排序函数
void heapSort(std::vector<std::pair<int, char>>& arr, int n) {
    // 构建最大堆
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);

    // 一个个取出元素，进行堆调整
    for (int i = n - 1; i > 0; i--) {
        std::swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

int main() {
    // 定义数组，元素是 pair，第一个元素是值，第二个元素是标识符
    std::vector<std::pair<int, char>> arr = {{5, 'a'}, {4, 'a'}, {3, 'a'}, {2, 'a'}, {4, 'b'}, {1, 'a'}};

    std::cout << "Original array:\n";
    printArray(arr);

    // 进行堆排序
    heapSort(arr, arr.size());

    std::cout << "\nSorted array:\n";
    printArray(arr);

    return 0;
}

结果输出如下，很明显4A和4B的关系在排序前后位置发生了变化。

Original array:
5a 4a 3a 2a 4b 1a 

Sorted array:
1a 2a 3a 4b 4a 5a

面试题：堆排序是一种稳定排序吗？

# 面试题：堆排序是一种稳定排序吗？

# 堆排序的稳定性分析

面试题：堆排序是一种稳定排序吗？

堆排序的稳定性分析