计算机基本架构-组合逻辑电路回顾
计算机基本架构-组合逻辑电路回顾
逻辑门是数字设计的基本元素,最终构成了数字系统的构建块。读者在深入了解计算机体系结构和设计细节之前,需要具备从基本逻辑门设计复杂逻辑块的扎实理解,并掌握设计过程中需要结合的设计工具和技术。
本章从定义逻辑门和真值表的概念开始,然后引出基本逻辑电路的实现。在本章后面,引入卡诺图的概念,以减少门电路数量,从而完成组合逻辑设计的基本要求。在最小化技术之后,介绍了各种基本逻辑模块,如多路复用器、编码器、解码器和一位加法器,以便它们可以用于构建更大规模的组合逻辑电路。本章的最后一部分专门介绍了巨型单元的设计。这些包括不同类型的加法器,如波纹进位加法器、前瞻进位加法器、选择进位加法器,以及根据设计目标(门数、电路速度和功耗)的组合类型。减法器、线性和桶形移位器、阵列和布斯乘法器构成本章的其余部分。
读者在学习本章及本书其余章节时,还需要投入时间学习硬件描述语言,如Verilog。这是至关重要的。结合Verilog的仿真平台和一套与Verilog配套的工具,如设计综合、静态时序分析和验证,是检查预期设计是否正确的有效方式。在专业设计环境中尝试各种设计理念,了解什么有效、什么无效,并使用不同的工具集,最重要的是从错误中学习,这是非常宝贵的经验。本书末尾附有一个附录,介绍Verilog的基本原理,供读者参考。
1.逻辑门
与门(AND)
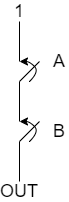
图1中的输出OUT在开关A和开关B都打开时为逻辑0。A和B有一个处于关闭状态,就会输出逻辑0。
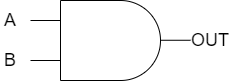
一个两输入的与门的功能与图1中的电路类似。如果图2中的与门的任意两个输入A和B,处于逻辑0,则与门会产生逻辑0的输出OUT。只有当与门的两个输入都等于逻辑1时,输出才会为逻辑1。该行为在表1中列出,这样的表称为真值表。
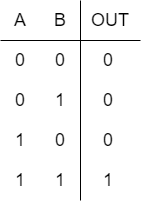
两个输入的与门的功能表示为:
OUT = A . B
这里,输入A和B之间的符号"."表示与操作。
或门(AND)
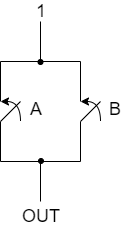
现在,假设开关A和B之间是并联连接,如图3所示。如果任意一个开关闭合,输出OUT将变为逻辑1;否则,输出将保持在逻辑0。
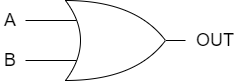
如图4所示的两输入或门的功能也类似于图3中的电路。如果任意两个输入为逻辑1,该门的输出OUT将为逻辑1。只有当门的两个输入都等于逻辑0时,输出才为逻辑0。这种行为在真值表(表2)中列出。
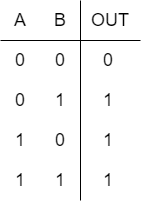
两个输入的或门的功能表示为:
OUT = A + B
这里,输入A和B之间的符号"+"表示或操作。
异或门
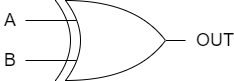
如图5所示,两输入异或门(XOR门)。如果两个输入相等,XOR门输出逻辑0。因此,在许多逻辑应用中,该门用于比较输入逻辑电平以判断它们是否相等。异或门的功能行为在表3中列出。
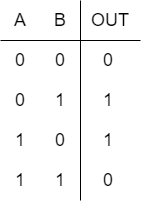
两个输入的异或门的功能表示为:
OUT = A ⊕ B
这里,输入A和B之间的符号"⊕"表示异或操作
缓冲器
缓冲器是一个单输入设备,其输出逻辑上等于其输入。该门的唯一用途是能够为连接到其输出的逻辑门输入提供足够的电流。该门的逻辑表示如图6所示。

互补逻辑门(反相器)
所有基本逻辑门都需要具有互补形式。如果需要对单个输入取反,使用如图7所示的反相器。反相器的真值表如表4所示。


反相器的功能表示为:
这里,输入IN上方的符号"-"表示取反的作用。
两输入与非门称为NAND门,其中N表示否定。其逻辑表示如图8所示,门输出端的圆圈表示补码输出。该门的真值表如表5所示。注意,该表中的所有输出值都是表1中给定值的完全相反。

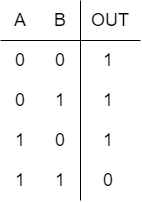
两个输入与非门的功能表示是:
与NAND门类似,两个输入的或门和异或门有相应的互补类型,分别称为两输入的或非门和异或非门。
两个输入的或非门的符号表示和真值表分别在图9和表6中显示。同样,表6中的所有输出都是表2中的互补。

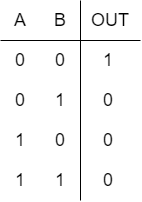
两个输入或非门的功能表示是:
图10和表7分别显示了两输入异或非门的符号表示和真值表。这个门与其对应的两输入异或门类似,常用于检测输入逻辑电平是否相等。
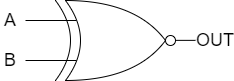
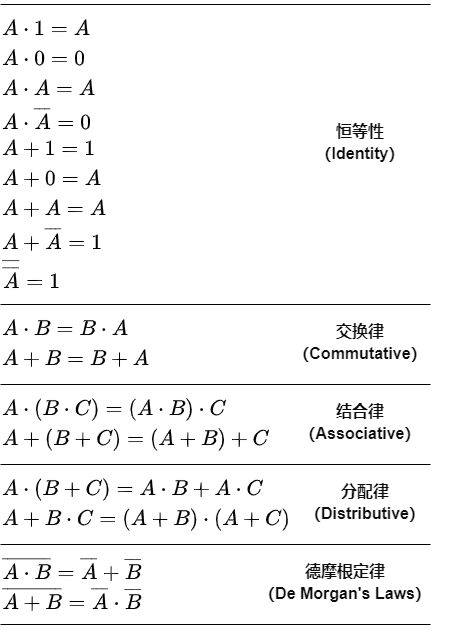
2.布尔代数
能够重新配置逻辑门以符合我们德设计目标是至关重要的。逻辑重配置可能像重新分组单个门的输入或对多个门的输入取反这样简单,以达到设计目标。
恒等律、交换律、结合律、分配律以及德摩根定律用于执行逻辑操作。下面这张表展示了这些定律。