第十讲：浮点数

由于历史原因，x86-64 有两个独立的浮点系统，它们之间的功能有一些重叠，但也有一些不同的功能。这两个系统是：

旧的 x87 协处理器指令集
较新的 XMM 矢量处理指令

无论哪种方式，浮点运算都使用一组完全不同的寄存器以及一组完全不同的操作。浮点值以二进制表示，其方式与有符号或无符号值完全不同。

浮点数的表示方法

我们可以使用三种浮点大小/表示形式，分别是 float（32 位）、double（64 位）和 long double（80 位，存储为 128 位，有 48 个未使用的填充位）。表示形式相似，唯一的区别是专用于数字每个部分的位数。实际的浮点格式（哪位执行什么操作）由名为 IEEE-754 的国际标准定义。

IEEE-754 浮点格式将小数值表示为三个字段的组合：

符号位 s，如果值为负则设置
指数 s，表示为（有偏差的）有符号二进制值。该值存储为实际指数加上固定偏差值 b。对于 32 位浮点值，偏差为 127。这意味着指数 0 在内部存储为 01111111b，-1 为 01111110b，1 为 10000000b，依此类推。
小数部分称为尾数 m，通常在 [1,2) 范围内（即 ≥ 1 但 < 2）。在标准化浮点值中，小数部分向左移动，因此第一个设置位被移出，因为该值的左侧几乎总是有一个隐式 1 位。（移动尾数需要增加/减少指数以保持相同的值。）

0 作为特殊情况处理。

使用这些字段的浮点数的值为

(-1s)(1 + m){2}^{e-b}

例如，浮点数 0.75 在二进制中是

0.110000000

指数为 ${2}^{0}$ 。然而，IEEE-754 要求我们将尾数向左移动，直到周期左侧的位被设置：

1.10000000 (mantissa, = 1.5)

要恢复其十进制值：

找到尾数的十进制值 (0.5) 并加上 1.0。（= 1.5）。
将尾数的十进制值乘以 2 指数
如果符号位为 1，则将十进制值乘以 -1。

二进制的表示

32位的浮点数的格式如下所示, 有1位是符号位，有8位是指数位，有23位是尾数。

s	exponent								mantissa
31	30	29	28	27	26	25	24	23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0

指数位是进行了+127的偏移，因此指数 0 将存储为 127 (= 01111111b)。这使得指数的范围是-127 到 + 128。

请注意，符号位位于高位，这意味着我们可以相对轻松地执行一些浮点操作。例如，要将浮点值转换为其绝对值（符号 = 0），只需将其与 0111…11 进行按位与即可。类似地，要确定浮点值是否为负，只需执行加载符号标志的操作。(例如，tst rax、rax）

尾数

尾数以二进制小数形式存储；最左端有一个隐含的 1 和小数点。因此:

10000000000000000000000b

实际上以十进制表示:

1 × {2}_{0} + 1 × {2}_{-1} + 0 × {2}_{-2} + ... = 1.5

1. 不与值一起存储，它是隐式的。

就像以二进制存储整数值时一样，我们将位乘以 2 的递增幂，然后将它们相加，这里我们将位乘以 2 的负幂和递减幂，然后将它们相加。

指数

指数有效地允许我们将尾数中的位向左或向右“移动”，同时将（隐式）小数点保持在同一位置。例如，要表示值 1.0，我们将使用尾数：

0.1000000000000000000000b = 0.5 (1.5 really)

但其指数为 10000000b = 1（无偏），

1.5 * 21 = 3.0 或 11.0000...b．

64位的表示方法

64 位和 80 位表示使用相同的基本原理，只是指数和尾数字段的大小不同：

Size	C/C++ type	Exponent size	Mantissa size
32-bit	float	8 bits	23 bits
64-bit	double	11 bits	52bits

80 位 long double表示略有不同：它使用15位指数，63位尾数，并且m的最高位中的隐含1实际上被存储，作为指数和尾数之间的位。该位称为整数位，它允许 0 具有更自然的表示形式，即全 0 的尾数（在 IEEE-754 格式中，表示尾数 1.0）。

IEEE-754 标准也定义了 128 位和 256 位浮点表示形式，但我们不用关心它们。

x87浮点数指令

以 f 开头的浮点指令是较旧的 x87 浮点指令集的一部分。它们使用一组单独的浮点寄存器 ST(0) 到 ST(7)，它们被视为栈。这些指令中的大多数不带操作数，并且隐式地对该堆栈的顶部元素进行操作。在YASM中，FP寄存器写为st0、st1等。

这种奇怪组织的原因是，最初所有浮点运算都是由物理上独立的协处理器 CPU 处理的。协处理器是一个独立的芯片，连接到总线，因此它能够“监听”。浮点指令由 CPU 分派到协处理器。(协处理器是可选的；尝试在没有它的情况下使用 FP 代码会触发异常)。因此，ST(x) 寄存器并不“驻留在”主 CPU 上，而是驻留在协处理器上，因此，为了更快，浮点计算必须尽可能地驻留在协处理器上。

如今，FP 寄存器栈与其他所有内容都位于同一 CPU 上，但为了与旧代码兼容，它仍然被视为单独的。使用 x87 指令的一个缺点是函数的浮点参数在 xmm 寄存器中传递，因此需要一些工作才能将它们放入 x87 子系统使用的 ST 寄存器中。然而，有些操作仅受 x87 子系统支持，因此可能值得付出努力。

所有 x87 浮点指令均以 f 开头，并且它们与使用 xmm 的指令之间存在一些重叠。如果两者都支持您想要的操作，那么您可以选择使用哪一个；如今两者都得到了同样的优化。由于 xmm 寄存器用于参数/返回值，因此可能需要一些额外的工作才能将值移入或移出 FP 寄存器堆栈。

在内部，x87 子系统将每个值存储为 80 位精度。当以浮点数或双精度数形式移入或移出内存时，值会向上/向下转换。这意味着我们“免费”获得额外的精度。（一般来说这是正确的：高精度和低精度浮点运算花费相同的时间，因此我们唯一关心的是空间使用情况。）

初始化

emms 用于通过重置其状态来初始化浮点协处理器。调用约定要求处理器在进入任何函数时处于 XMM 模式，因此为了安全起见，我们将始终在使用 x87 系统的任何函数的开头调用 emms。

浮点寄存器栈

x87系统有 8 个独立的、可寻址的 80 位数据寄存器 R0~R7，这些寄存器合称为浮点寄存器栈。

我们使用st0 ~ st7去使用浮点寄存器栈。st后方的数字代表的是到栈顶的距离，st0代表的是栈顶。大多数 x87 指令隐式使用 st0 作为其操作的目标（例如，fsub 将其结果写入 st0。）所有 ST 寄存器均由调用者保存(caller-preserved)。 x87 浮点代码基本上可以归结为管理这些寄存器。

浮点栈也有类似的push和pop操作：

浮点栈的pop操作会执行下面的两步：

翻转所有的浮点寄存器。让st0指向st1，让st1指向st2，以此类推。
将st0标记为空闲。
pop

浮点栈的push操作会执行下面的两步：

反向翻转所有的浮点寄存器。
将st0标记为使用中。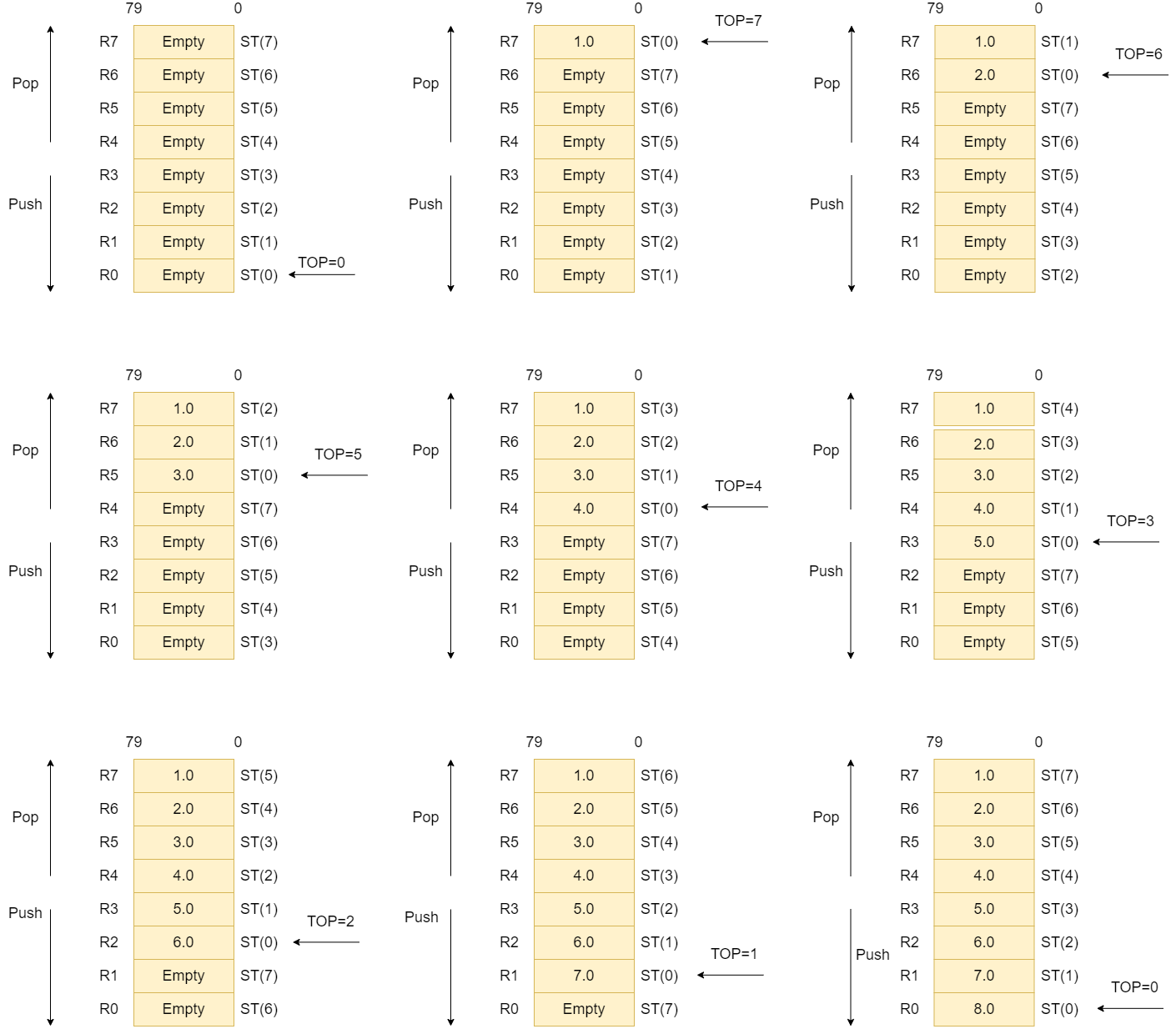
push

上述过程，相对比较抽象，我们通过一个实际的例子来感受一下浮点寄存器栈push和pop的过程。

这里会使用fld指令和fstp指令，可以将其暂时理解为push和pop。

section .data

v1: dd 1.0
v2: dd 2.0

section .text
global _start
_start:
  fld dword [v1]
  fld dword [v2]

  fstp    dword [v1]
  fstp    dword [v2]

  mov     rax,    60              ; Syscall code in rax
  mov     rdi,    0               ; First parameter in rdi
  syscall                         ; End process

进行编译：

yasm -g dwarf2 -f elf64 hello.s -l hello.lst
ld -g -o hello hello.o

使用gdb进行调试，使用info float显示寄存器栈的使用情况。

[root@localhost lecture10]# gdb hello -q
Reading symbols from hello...
(gdb) list
1       section .data
2
3       v1: dd 1.0
4       v2: dd 2.0
5
6       section .text
7       global _start
8       _start:
9         fld dword [v1]
10        fld dword [v2]
(gdb)
11
12        fstp    dword [v1]
13        fstp    dword [v2]
14
15        mov     rax,    60              ; Syscall code in rax
16        mov     rdi,    0               ; First parameter in rdi
17        syscall                         ; End process
(gdb)
Line number 18 out of range; hello.s has 17 lines.
(gdb) b 9
Breakpoint 1 at 0x401000: file hello.s, line 9.
(gdb) r
Starting program: /home/work/assembly/lecture10/hello

Breakpoint 1, _start () at hello.s:9
9         fld dword [v1]
(gdb) info float
  R7: Empty   0x00000000000000000000
  R6: Empty   0x00000000000000000000
  R5: Empty   0x00000000000000000000
  R4: Empty   0x00000000000000000000
  R3: Empty   0x00000000000000000000
  R2: Empty   0x00000000000000000000
  R1: Empty   0x00000000000000000000
=>R0: Empty   0x00000000000000000000

Status Word:         0x0000
                       TOP: 0
Control Word:        0x037f   IM DM ZM OM UM PM
                       PC: Extended Precision (64-bits)
                       RC: Round to nearest
Tag Word:            0xffff
Instruction Pointer: 0x00:0x00000000
Operand Pointer:     0x00:0x00000000
Opcode:              0x0000
(gdb) si
10        fld dword [v2]
(gdb) info float
=>R7: Valid   0x3fff8000000000000000 +1
  R6: Empty   0x00000000000000000000
  R5: Empty   0x00000000000000000000
  R4: Empty   0x00000000000000000000
  R3: Empty   0x00000000000000000000
  R2: Empty   0x00000000000000000000
  R1: Empty   0x00000000000000000000
  R0: Empty   0x00000000000000000000

Status Word:         0x3800
                       TOP: 7
Control Word:        0x037f   IM DM ZM OM UM PM
                       PC: Extended Precision (64-bits)
                       RC: Round to nearest
Tag Word:            0x3fff
Instruction Pointer: 0x00:0x00401002
Operand Pointer:     0x00:0x00000000
Opcode:              0x0000
(gdb) si
12        fstp    dword [v1]
(gdb) info float
  R7: Valid   0x3fff8000000000000000 +1
=>R6: Valid   0x40008000000000000000 +2
  R5: Empty   0x00000000000000000000
  R4: Empty   0x00000000000000000000
  R3: Empty   0x00000000000000000000
  R2: Empty   0x00000000000000000000
  R1: Empty   0x00000000000000000000
  R0: Empty   0x00000000000000000000

Status Word:         0x3000
                       TOP: 6
Control Word:        0x037f   IM DM ZM OM UM PM
                       PC: Extended Precision (64-bits)
                       RC: Round to nearest
Tag Word:            0x0fff
Instruction Pointer: 0x00:0x00401007
Operand Pointer:     0x00:0x00000000
Opcode:              0x0000
(gdb) si
13        fstp    dword [v2]
(gdb) info float
=>R7: Valid   0x3fff8000000000000000 +1
  R6: Empty   0x40008000000000000000
  R5: Empty   0x00000000000000000000
  R4: Empty   0x00000000000000000000
  R3: Empty   0x00000000000000000000
  R2: Empty   0x00000000000000000000
  R1: Empty   0x00000000000000000000
  R0: Empty   0x00000000000000000000

Status Word:         0x3800
                       TOP: 7
Control Word:        0x037f   IM DM ZM OM UM PM
                       PC: Extended Precision (64-bits)
                       RC: Round to nearest
Tag Word:            0x3fff
Instruction Pointer: 0x00:0x0040100e
Operand Pointer:     0x00:0x00000000
Opcode:              0x0000
(gdb) si
15        mov     rax,    60              ; Syscall code in rax
(gdb) info float
  R7: Empty   0x3fff8000000000000000
  R6: Empty   0x40008000000000000000
  R5: Empty   0x00000000000000000000
  R4: Empty   0x00000000000000000000
  R3: Empty   0x00000000000000000000
  R2: Empty   0x00000000000000000000
  R1: Empty   0x00000000000000000000
=>R0: Empty   0x00000000000000000000

Status Word:         0x0000
                       TOP: 0
Control Word:        0x037f   IM DM ZM OM UM PM
                       PC: Extended Precision (64-bits)
                       RC: Round to nearest
Tag Word:            0xffff
Instruction Pointer: 0x00:0x00401015
Operand Pointer:     0x00:0x00000000
Opcode:              0x0000

info float命令非常形象的显示了压栈和出栈操作的过程。

加载

在 x87 术语中，将值压入栈称为加载(loading)。从内存加载浮点数到浮点栈中有下面这些方法：

fld  dword [addr]   ; Push float from memory
fld  qword [addr]   ; Push double from memory
fld  st1            ; Push st1 to st0

fild dword [addr]   ; Push signed dword integer from memory
fild qword [addr]   ; Push signed qword integer from memory

fld1        ; Push +1.0
fldz        ; Push +0.0
fldpi       ; Push π

请注意，所有这些压栈操作不仅将 st0 设置为期望的值，还将旧的 st0 及其下面的所有内容向下移动。

还有一些其他可以推送的常量；请参阅了解完整列表open in new window。

没有加载浮点立即数的指令。要加载浮点常量，除了专用指令之外的浮点常量，您必须将其存储在内存中（通常在 .data 或 .rodata 中），然后从那里加载它。一些简单的常量可以从 fld1 和 fldz 指令支持的 1,0 中合成出来。

许多指令都有 -p 形式，它也会在执行操作后弹出栈。例如:

fst st3 将 ST(0) 复制到 ST(3)，而 fstp st3 执行相同的操作，但随后执行pop操作。

为了更方便地操作堆栈较低的值，fxch 指令将另一个 st 寄存器中的值与 st0 交换。例如:

fxch st3    ; Swap st0 with st3

写入memory

将 FP 栈的结果写回内存称为存储(store)。

fst/fstp用于将浮点值从st0移动到栈中的其他位置，或从st0移动到内存中。

fst  dword [addr]  ; Copy float st0 to [addr]
fst  st1           ; Copy st0 to st1
fstp st1           ; Copy st0 to st1 and then pop

请注意，对于存储到内存，需要大小限定符（dword 或 qword），以便汇编器知道是复制为 float 还是 double。

我们还可以通过四舍五入或截断来存储整数：

fist   dword [addr]     ; Write float ST(0) as integer to addr
fistp  dword [addr]     ; Write float ST(0) as integer and then pop
fisttp qword [addr]     ; Write double as trunc. integer and then pop

（64 位存储只能在 -p popping 变体中完成。）

舍入使用当前舍入模式，而截断只是丢弃任何小数部分，有效地向 0 舍入。

算术运算

大多数算术运算有几种形式：

单个参数（st 寄存器或内存操作数），st0 作为隐式目标。例如:

fmul st2       ; st0 = st0 * st2

两个参数，两者都是 ST 寄存器，其中之一是 st0。例如：

fmul st2, st0  ; st2 = st2 * st0

两个寄存器之一必须是 st0。您不能（例如）将 st2 乘以 st3。

没有三个参数的形式，因此不能直接执行 st0 = st1 + st2。

主要的算术运算有:

fadd      ; Addition
fsub      ; Subtraction
fmul      ; Multiplication
fdiv      ; Division

所有这些指令都有下面三种形式：

op stx（st0 = st0 op stx，例如fadd st3, st0 = st0 + st3 ）、
op st0, stx（st0 = st0 op stx, 同上）
op stx, st0（stx = stx op st0，例如fadd st3,st0 st3 = st3 + st0）

除法和减法也有反向（fsubr，fdivr）形式可用，其计算的是st0 = st(x) - st(0)，而不是st0 = st0 - st(x)）。还有一些整数变体，它们将第二操作数读为内存的整数。

浮点函数参数

因为 ABI 要求在 xmm 寄存器中传递普通浮点参数，所以需要一些工作才能将它们放入 FP 栈。我们必须将它们移动到内存中（通常是在堆栈上分配的本地空间），然后从那里加载到 FP 堆栈中。例如，在带有两个浮点参数的函数中：

func:
  ; xmm0 = argument 1
  ; xmm1 = argument 2

  push rbp
  mov rbp, rsp  

  movsd qword [rsp-8],  xmm0
  movsd qword [rsp-16], xmm1

  ; Switch to x87 mode
  emms

  fld qword [rsp-8]   ; Push xmm0 
  fld qword [rsp-16]  ; Push xmm1

  ; Now arg 1 is in st1, arg 2 is in st0

  ...

  add rsp, 16
  pop rbp
  ret

请注意，我们使用红色区域（rsp 上方的 128 个字节）来进行传输，以避免必须在栈上显式分配空间。这种"临时内存"的使用正是红色区域存在的原因。）

返回一个浮点值，当该值存在于 FP 堆栈中时，同样涉及到内存的往返，以便将其放入 xmm0 中。例如，返回 st0：

fstp    qword [rsp-8]   ; pop from st0 onto the top of the stack
movsd   xmm0, [rsp-8]   ; load top of stack into xmm0

这里再次使用红色区域作为临时存储。

当从使用 x87 浮点的函数返回时，您需要释放（即标记为空）所有 FP 寄存器，通常通过执行

fstp st0
fstp st1

浮点数的比较

fcomi 指令比较两个 FP 堆栈元素（其中第一个必须是 st0）并像无符号比较一样更新标志寄存器。x87 系统有自己的内部标志寄存器，原始 fcom 指令将更新该寄存器；然后将 x87 标志放入普通标志寄存器中，然后就可以使用普通的条件跳转指令了。例如，将 st0 和 st1 中较大的一个复制到 st0 中：

  fcomi st0, st1   ; Compare st0, st1
  jge  .done       ; Jump to .done if st0 >= st1
  fld  st1         ; Otherwise push st0 = st1

.done:

fcmov__ 系列执行条件（浮点）移动，类似于 cmov__ 系列。

例如，将 st0 和 st1 中较大的一个复制到 st1

fcomi   st0, st1     ; Compare st0 with st1
fcmovl  st1          ; Set st0 = st1 if st0 < st1

讽刺的是，没有无条件 FP 移动指令可以执行相同的操作（将 st0 设置为另一个 st 寄存器的值）！我们能做的就是push.（XMM 浮点系统有一条指令可以查找两个值中的最大值。）

fcomip 进行比较然后弹出。 fucomi 进行“无序”比较；当操作数之一为非数字时，无序比较的结果会有所不同：

操作数不是数字:

在有序比较中，NaN 与其他数字之间的比较会导致浮点异常。
在无序比较中，NaN 与其他数字之间的比较始终给出真实结果。即，NaN 算作小于、大于、等于和不等于所有其他数字！

通常我们更喜欢无序比较，因为它稍微快一些，并且意味着我们不必处理浮点异常。

要与常量 0.0 进行比较，请使用 ftst，它将 st0 与 0 进行比较。这样您就不必将常量 0 加载到其他寄存器之一进行比较。

数学运算

x87 子系统具有许多常见数学函数的单指令。大部分这些功能在XMM 系统中是没有的，这也是去使用 x87 系统的原因之一。

; Trig functions
fsin         ; st0 = sin(st0)
fcos         ; st0 = cos(st0)
fsincos      ; st0 = sin(st0), push cos(st0)
fptan        ; st0 = tan(st0), push 1.0
fpatan       ; st1 = atan(st1 / st0) and then pop

fsqrt        ; st0 = sqrt(st0)

fprem1       ; st0 = fmod(st0, st1) (fractional remainder)

fabs         ; st0 = |st0| (absolute value)

fyl2x        ; st1 = st1 × log₂(st0)
f2xm1        ; st0 = 2^st0 - 1

使用以 2 为底的对数/指数是因为考虑到浮点数使用的二进制格式，这些相对容易计算。可以通过使用熟悉的对数恒等式来使用其他底数。

在 x87 和 XMM 模式之间切换

当使用x87系统时，我们必须发出emms指令来清除XMM状态。然而当使用 XMM 系统时，则不需要特定的初始化指令。

浮点数的例子：计算π

这里我们将使用著名的 π 级数近似:

=4\sum _{i=0} {\frac {-{1}^{i}} {2i+1}}=1-\frac {1} {3}+\frac {1} {5}-...

我们将继续这个系列，直到连续值之间的差异小于 0.000001（即 5 位精度），然后使用 C 标准库中的 printf 打印结果。

在本例中，我们将使用 x87 浮点系统，尽管因为 printf 期望其浮点参数位于 xmm 寄存器中，所以我们必须将正在计算的值从 x87 堆栈移动到内存中，然后从那里移动到xmm0。

在 C 语言中，我们要编写的函数如下所示:

double pi() {
    double p = 0.0;   // Current pi approximation
    double pp = 0.0;  // Previous pi approximation
    double s = 1;     // Sign: +1 or -1
    double d = 1;     // Denominator: 1,3,5,...

    do {
        pp = p;        
        p += s / d;
        s *= -1;
        d += 2;        
    } while(abs(p - pp) > 0.000001);

    return 4 * p;
}

请注意，p - pp == s / d。

虽然可以通过一些技巧来编写此过程，使其完全在 x87 堆栈上运行，但为了获得最大速度，最简单的编写方法是将变量存储在堆栈上（在红色区域中），然后加载/根据需要存储它们。当然，我们必须将浮点常量 2 和 0.000001 保存在 .data 部分中：

section .data

ZERO:       dq      0.0
ONE:        dq      1.0
TWO:        dq      2.0
EPSILON:    dq      0.000001

section .text

pi:
    push    rbp
    mov     rbp, rsp

    ; In the red zone
    ; [rsp - 8]  = p = 0.0
    ; [rsp - 16] = s = 1
    ; [rsp - 24] = d = 1
    ; [rsp - 32] = s / d

    mov     rax, qword [ZERO]
    mov     qword [rsp - 8], rax

    mov     rax, qword [ONE]
    mov     qword [rsp - 16], rax
    mov     qword [rsp - 24], rax

.begin_loop:
    ; Update p += s / d
    fld     qword [rsp - 16]       ; = s
    fdiv    qword [rsp - 24]       ; = s / d
    fst     qword [rsp - 32]       ; Save s / d for later
    fadd    qword [rsp - 8]        ; = s / d + p
    fstp    qword [rsp - 8]        ; Write back 
    ffree   st0

    ; Update s = -s
    fld     qword [rsp - 16]        ; st0 = s
    fchs                            ; st0 = -st0
    fst     qword [rsp - 16]        ; Write back
    ffree st0

    ; Update d += 2
    fld     qword [TWO]
    fld     qword [rsp - 24]
    fadd    st0, st1                ; st0 += 2
    fstp    qword [rsp - 24]        ; Write back
    ffree   st0

    fld     qword [rsp - 32]
    fabs
    fld     qword [EPSILON]         ; st0 = 0.000001, st1 = |s / d|
    fucomi  st1                     ; Compare st0, st1
    ffree   st0                     ; Remove st0, st1 from the stack
    ffree   st1

    jb .begin_loop                  ; loop if 0.0000001 > |s / d|

    ; Multiply result by 4
    fld qword [TWO]
    fld qword [rsp - 8]
    fmul st0, st1
    fmul st0, st1
    fstp qword [rsp - 8]
    ffree st0    

    ; Copy last p into xmm0
    movsd xmm0, qword [rsp - 8]

    pop rbp
    ret

关于清除（ffree）堆栈元素的注意事项：确保 x87 堆栈上的元素不超过 8 个非常重要。如果你压入超过 8 个东西而不弹出，ST(8) 最终将回绕到 ST(0) 并且堆栈将被损坏。这通常会表现为值“神奇地”变成 NaN。例如，如果我们在循环结束时没有执行 ffree 指令，堆栈的大小将无限增长，直到最终覆盖自身。

XMM 浮点指令

CPU 上的现代浮点单元及其专用寄存器与向量 (SIMD) 单元（以及旧的 x87 单元）共享资源。事实上，大多数现代浮点实际上是矢量化浮点代码。正如我们将要做的那样，真正的代码很少一次只对一个值进行操作。

寄存器

有 16 个浮点寄存器，名为 xmm0到 xmm15。这些寄存器的大小实际上均为 128 位，但我们将仅使用 32 位或 64 位部分，这对应于我们正在使用的浮点大小。一般来说，后缀 s 用于表示单精度（float），而后缀 d 用于表示双精度（double）。

xmm0 到 xmm7 用于传递浮点参数。 xmm8-15 是临时（调用者保存的）寄存器。

移动浮点值

movss dest, src         ; Move floats
movsd dest, src         ; Move doubles

两个专用的 mov 指令用于移动浮点值。像往常一样，两个操作数必须具有相同的大小，并且大小必须与指令匹配。目标和源可以是内存或（xmm）寄存器，但不能同时是内存。与普通的 mov 指令不同，源不能是立即数。要将常量浮点值加载到寄存器中，它必须已经存在于内存中。请注意，寄存器操作数必须是浮点寄存器。

在 `.data` 中存储浮点值

使用dd（双字）存储32位浮点值，使用dq（四字）存储64位值。例如：

section .data

pi:     dq      3.14159

浮点转换

存在用于在 32 位和 64 位格式之间进行转换以及将整数转换为浮点值的指令，反之亦然。

算术

addss dest, src         ; dest += src (float)
addsd dest, src         ; dest += src (double)
subss dest, src         ; dest -= src (float)
subsd dest, src         ; dest -= src (double)
mulss dest, src         ; dest *= src (float)
mulsd dest, src         ; dest *= src (double)
divss dest, src         ; dest /= src (float)
divsd dest, src         ; dest /= src (double)

所有这些的三操作数版本都带有 v 前缀：

vaddss dest, src1, src2  ; dest = src1 + src2
vaddsd dest, src1, src2  ; dest = src1 + src2
vsubss dest, src1, src2  ; dest = src1 + src2
vsubsd dest, src1, src2  ; dest = src1 + src2
vmulss dest, src1, src2  ; dest = src1 + src2
vmulsd dest, src1, src2  ; dest = src1 + src2
vdivss dest, src1, src2  ; dest = src1 + src2
vdivsd dest, src1, src2  ; dest = src1 + src2

dest和src操作数必须是xmm寄存器； src2 可以是寄存器或内存。所有操作数的大小必须相同。

提供了许多更高级的数学运算作为说明：

指令	描述
`sqrtss dest, src` `sqrtsd dest, src`	`dest = sqrt(src)` 开根号
`rcpss dest, src`	`dest = 1/src`
`rsqrtss dest, src`	`dest = 1/sqrt(src)`
`maxss dest, src` `maxsd dest, src`	dest =maximum of dest, src
`minss dest, src` `minsd dest, src`	dest =minimum of dest, src
`roundss dest, src, mode`	Round src into dest using mode mode = 0 ties go to even mode = 1 round down mode = 2 round up mode = 3 round toward 0

（但请注意，使用 x87 可用的三角函数此处不可用。）

浮点比较

特殊的浮点比较指令用于比较两个浮点操作数，但是结果被写入普通标志寄存器，就像无符号比较一样。因此，条件跳转指令 je、jne、ja、jae、jb 和 jb 可用于在等于、不等于、大于、大于或等于、小于和小于时跳转。

ucomiss dest, src           ; Compare dest and src (dest must be float reg.),
ucomisd dest, src           ; setting rif as for an unsigned comparison

浮点系统拥有自己的标志/状态寄存器，称为 mxcsr。这里的标志不是由浮点指令设置，而是由我们在浮点指令之前设置并控制全局行为，例如舍入模式、除以零是否应产生异常或仅产生无穷大等。

与 x87 一样，我们在这里执行无序比较，这意味着操作数之一为非数字的任何比较都会给出真实结果。

函数的浮点参数

System-V 调用约定指定函数的前 8 个浮点参数在寄存器 xmm0 到 xmm7 中传递。结果（如果有）在 xmm0 中返回。所有浮点寄存器都是调用者保留的(caller-saved)，这意味着在调用任何函数之前必须将它们压入栈。

需要注意的重要一点是：如果您使用 printf，%f 格式说明符实际上需要一个双精度（64 位）参数，而不是浮点数。当我们在示例中使用 printf 时，我们必须使用 cvtss2sd 将浮点值转换为双精度值以进行打印。

像 printf 这样采用可变数量参数的函数需要进行额外的更改：xmm 寄存器中的参数数量必须在 al 中设置。

浮点数的例子：计算π

这里我们将使用著名的 π 级数近似:

=4\sum _{i=0} {\frac {-{1}^{i}} {2i+1}}=1-\frac {1} {3}+\frac {1} {5}-...

我们将继续这个系列，直到连续值之间的差异小于 0.000001（即 5 位精度），然后使用 C 标准库中的 printf 打印结果。

在 C 语言中，我们要编写的函数如下所示:

float pi() {
    float p = 0.0;   // Current pi approximation    
    float s = 1;     // Sign: +1 or -1
    float d = 1;     // Denominator: 1,3,5,...
    float rd;        // 1 / d

    do {
        rd = 1 / d;
        p += s * rd;
        s *= -1;
        d += 2;        
    } while(abs(sd) > 0.000001);

    return 4 * p;
}

与 x87 版本不同，没有指令翻转 xmm 寄存器的符号，或获取 xmm 寄存器的绝对值。因此，我们要克服一些困难：

翻转符号对应于乘以-1。
我们不取绝对值，而是计算 1/d 并保存其值以供比较，然后再乘以交替符号。

由于 xmm 寄存器同时用于整数和浮点数学，因此可以通过直接修改寄存器中的位来伪造绝对值和符号翻转：

SIGN_BIT:   equ         (1 << 63)

    pxor    xmm0, qword [SIGN_BIT]      ; Flip sign bit
    pandn   xmm0, qword [SIGN_BIT]      ; Clear sign bit

将其转换为汇编为我们提供了一个简单的循环：

section .data

zero:   dd      0.0
one:    dd      1.0
two:    dd      2.0
four:   dd      4.0
negone: dd      -1.0
limit:  dd      0.000001


format: db      "%f", 10, 0

section .text

extern printf

global main
main:

    push rbp
    mov rbp, rsp

    ;; Compute pi    
    call compute_pi
    ; Return value in xmm0  

    ;; Print result
    mov rdi, format
    mov al, 1
    cvtss2sd xmm0, xmm0 ; Convert to double for printf
    call printf

    mov rax, 0
    pop rbp
    ret

compute_pi:
    push rbp
    mov rbp, rsp

    movss xmm7, dword [one]  ; 1.0
    movss xmm0, dword [zero] ; p = 0
    movss xmm1, xmm7   ; s = 1
    movss xmm2, xmm7   ; d = 1
    ; xmm3 = t

.loop:
    movss xmm3, xmm7                ; t = 1
    divss xmm3, xmm2                ; t /= d
    vmulss xmm4, xmm1, xmm3         ; xmm4 = s * t
    addss xmm0, xmm4                ; p += s * t
    mulss xmm1, dword [negone]      ; s *= -1
    addss xmm2, dword [two]         ; d += 2

    ucomiss xmm3, dword [limit]     ; while(t > limit)
    ja .loop

    ; Result is in xmm0
    mulss xmm0, dword [four]

    pop rbp
    ret

当我们调用 printf 时，我们必须做一个小的调整：采用可变数量参数的函数（如 printf）要求我们将 al 设置为 xmm 寄存器中传递的参数数量。它不必精确，但 al 应该 ≥ 用于参数的 xmm 寄存器的数量。到目前为止，我们从未在 xmm 中传递过任何内容，所以这并不重要。然而现在，我们必须在调用 printf 之前设置 al = 1，以便 printf 知道要使用多少个。

浮点数的其他知识点

我们重点关注两种浮点格式，分别对应于 float（32 位）和 double（64 位）

section .data

zero:   dd      0.0
one:    dd      1.0
two:    dd      2.0
four:   dd      4.0
negone: dd      -1.0
limit:  dd      0.000001


format: db      "%f", 10, 0

section .text

extern printf

global main
main:

    push rbp
    mov rbp, rsp

    ;; Compute pi    
    call compute_pi
    ; Return value in xmm0  

    ;; Print result
    mov rdi, format
    mov al, 1
    cvtss2sd xmm0, xmm0 ; Convert to double for printf
    call printf

    mov rax, 0
    pop rbp
    ret

compute_pi:
    push rbp
    mov rbp, rsp

    movss xmm7, dword [one]  ; 1.0
    movss xmm0, dword [zero] ; p = 0
    movss xmm1, xmm7   ; s = 1
    movss xmm2, xmm7   ; d = 1
    ; xmm3 = t

.loop:
    movss xmm3, xmm7          ; t = 1
    divss xmm3, xmm2          ; t /= d
    vmulss xmm4, xmm1, xmm3   ; xmm4 = s * t
    addss xmm0, xmm4          ; p += s * t
    mulss xmm1, dword [negone]      ; s *= -1
    addss xmm2, dword [two]         ; d += 2

    ucomiss xmm3, dword [limit]     ; while(t > limit)
    ja .loop

    ; Result is in xmm0
    mulss xmm0, dword [four]

    pop rbp
    ret

附录

课程原文：https://staffwww.fullcoll.edu/aclifton/cs241/lecture-floating-point-simd.htmlopen in new window

浮点数工具： https://baseconvert.com/ieee-754-floating-pointopen in new window

浮点数： https://polarisxu.studygolang.com/posts/basic/diagram-float-point/open in new window

x87编程： http://www.infophysics.net/x87.pdfopen in new window

第十讲：浮点数

# 第十讲：浮点数

# 浮点数的表示方法

# 二进制的表示

# 尾数

# 指数

# 64位的表示方法

# x87浮点数指令

# 初始化

# 浮点寄存器栈

# 加载

# 写入memory

# 算术运算

# 浮点函数参数

# 浮点数的比较

# 数学运算

# 在 x87 和 XMM 模式之间切换

# XMM 浮点指令

# 寄存器

# 移动浮点值

# 在 .data 中存储浮点值

# 浮点转换

# 算术

# 浮点比较

# 函数的浮点参数

# 浮点数的其他知识点

# 附录

第十讲：浮点数

浮点数的表示方法

二进制的表示

尾数

指数

64位的表示方法

x87浮点数指令

初始化

浮点寄存器栈

加载

写入memory

算术运算

浮点函数参数

浮点数的比较

数学运算

在 x87 和 XMM 模式之间切换

XMM 浮点指令

寄存器

移动浮点值

在 `.data` 中存储浮点值

浮点转换

算术

浮点比较

函数的浮点参数

浮点数的其他知识点

附录